Snowflake
Introduzione
Il fiocco di neve di Koch è uno degli esempi più famosi di frattali: figure geometriche affascinanti che presentano una struttura auto-simile a qualsiasi livello di ingrandimento. Tale frattale deve il suo nome al matematico svedese Helge von Koch, che lo introdusse nel 1904 come esempio di curva continua ma non derivabile. Questa figura rappresenta una delle prime esplorazioni della geometria frattale, molto prima che il termine “frattale” fosse coniato da Benoît Mandelbrot nel 1975.
Von Koch descrisse la curva come una dimostrazione di come sia possibile costruire una figura con una lunghezza infinita che racchiude una superficie finita. Questa proprietà “paradossale” catturò l’attenzione dei matematici e divenne un punto di riferimento per lo studio dei frattali e della loro applicazione nella matematica moderna. La curva di Koch viene generata applicando ripetutamente una semplice regola geometrica a un triangolo equilatero di base. Il risultato è una figura che, con ogni iterazione, diventa sempre più complessa, rivelando dettagli sorprendenti.
Risultato
Ecco il risultato visivo del codice sottostante, rappresentato tramite un’animazione che mostra i primi cinque livelli del frattale:
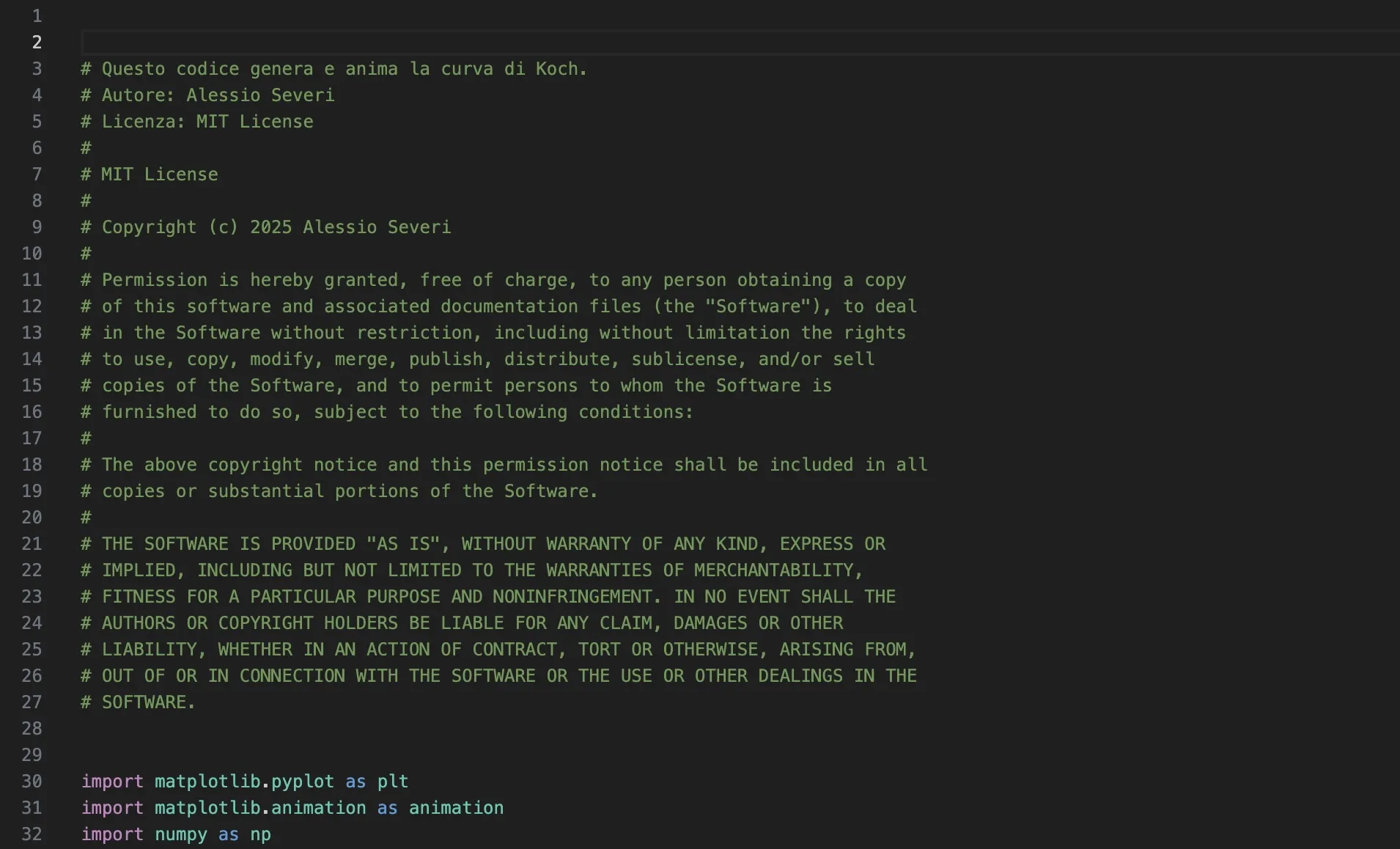
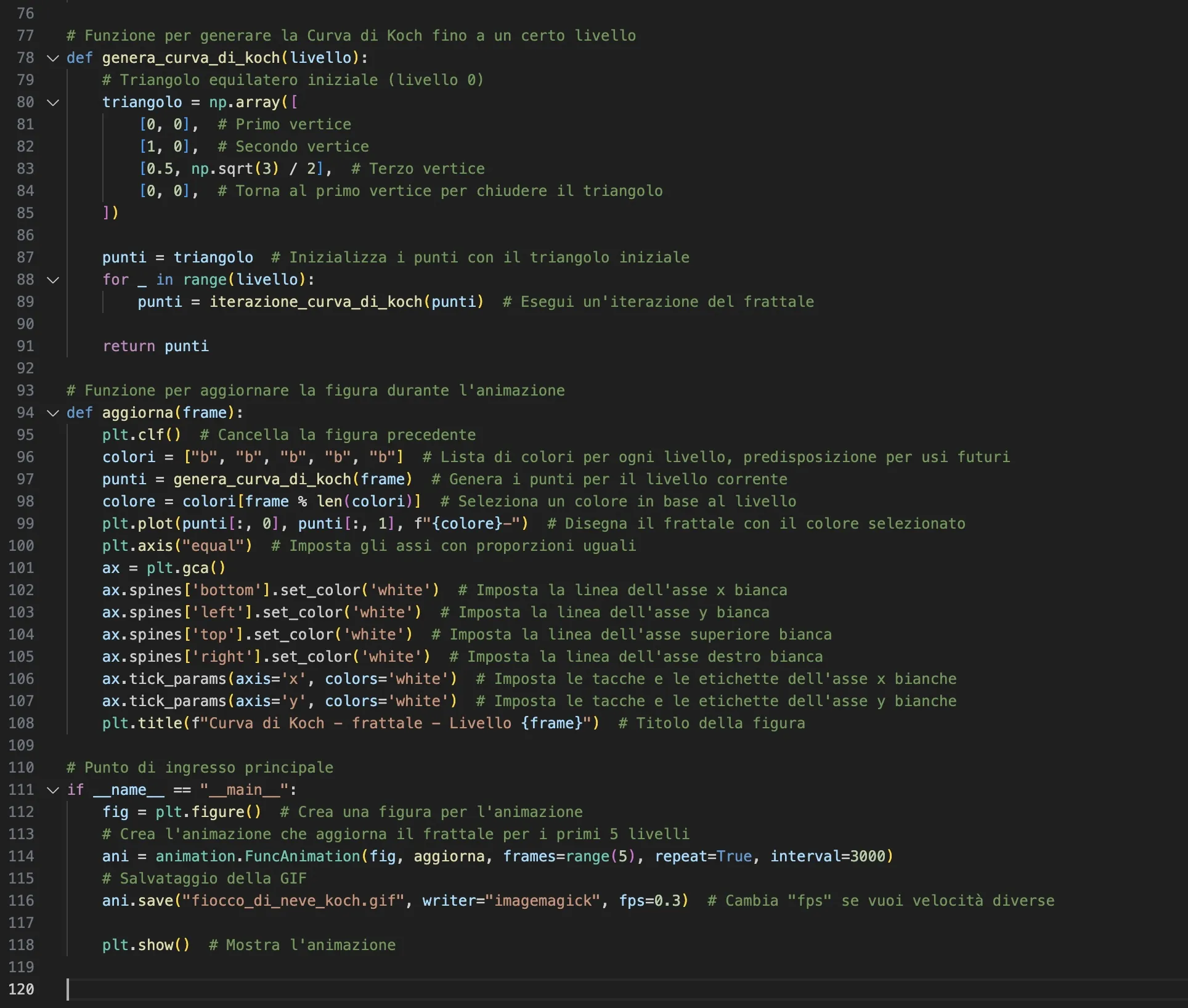
Codice
Il codice che segue, scritto in Python, non solo mostra come calcolare e rappresentare la curva di Koch, ma la anima, mostrando visivamente il processo di generazione del frattale passo dopo passo. Questa animazione è un ottimo strumento per chiunque voglia esplorare le meraviglie della geometria frattale o per insegnare i concetti fondamentali della ricorsione e della suddivisione geometrica.